前言
昨天看到抖音上有人关于头相尾的快捷计算方法,觉得确实有趣。不过,我从高中时也是无意间从一本书上看到的简便计算方法,从那时开始我就一直在用,到现我都不知道这种计算有没有名字。确实要比按照常规计算要容易一些,而且会快一些。
但总的来说,万变不离其宗,不管是怎么样的计算方法,它都是遵从计算的基本原理,然后从中找出的规律来总结出来的。
通用的两位数计算法
如图如示

计算过程 (数a x 数b)
1. 个位相乘: a个位数 x b个位数 = 结果1,结果1以个位为基数
2. 十位相乘: a十位数 x b十位数 = 结果2,结果2以百位为基数
3. 交叉相乘: a十位数 x b个位数 + b十位数 X a个位数 = 结果3,结果3以十位为基数
4. 总和结果: 结果1 + 结果2 + 结果3 = 总结果
综述
* 其实只要细细一想,它跟基本的计算方法是一脉相承的
* 可以减少进位数在常规计算中造成的错误
* 降低了一些常规计算中的思维处理细节,仅仅只有第3步会在数大的时候
* 通用于2位数的相乘计算
总之,它确实从一定的方面简化了计算难度,减少了常规计算中容易造成的错误。
头同尾补
头同就是十位数都一样的,尾补就是个位两数之和刚好是10.所以了,这种计算就是要先判断条件是否满足。

- (相同的十位数 + 1)x 相同的十位数 = 结果1,结果1以百位为基数
- 两尾数相乘 = 结果2,结果2以个位为基数
- 总和结果 = 结果1 + 结果2
a乘数互补,b乘数数字相同
即一个乘数的十位数和个位数互补,另一个乘数的十位数跟个位数相同。
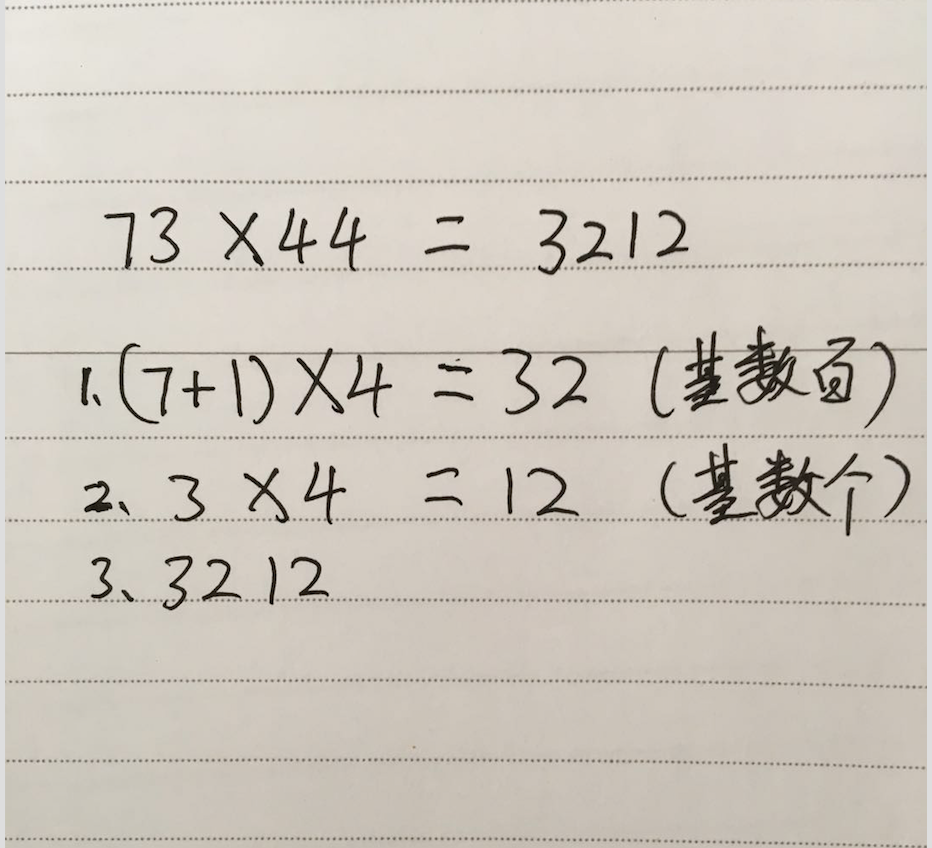
- (a的十位数 + 1)x b的十位数 = 结果1,结果1以百位为基数
- a的个位数 x b的个位数 = 结果2,结果2以个位为基数
- 总和结果 = 结果1 + 结果2
其他几种
十几乘十几
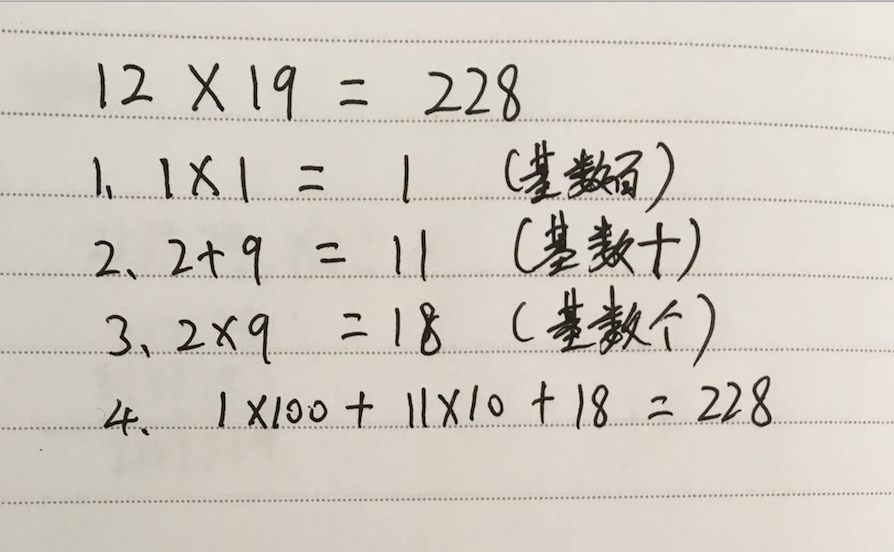
- 两数十位数相乘 = 结果1,结果1以百位为基数
- 两数个位数相加 = 结果2,结果2以十位为基数
- 两数个位数相乘 = 结果3,结果3以个位为基数
- 总和结果 = 结果1 + 结果2 + 结果3
几十一乘几十一

- 两数十位数相乘 = 结果1,结果1以百位为基数
- 两数十位数相加 = 结果2,结果2以十位为基数
- 两数个位数相乘 = 结果3,结果3以个位为基数
- 总和结果 = 结果1 + 结果2 + 结果3
任意数 x 11
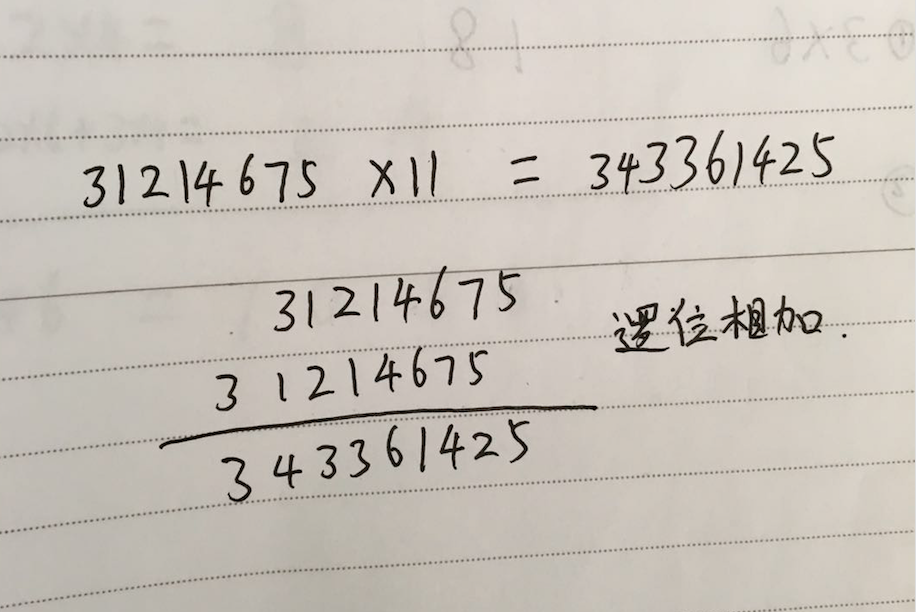
任意数逻位相加
可扩展到 乘数为11 ,111,1111……,其中只是逻的数的个数不同。
总结
总之,除此之外还有一些方法,但是相乘的实质都是一样的,这些方法只是在特殊情况下可以运用这些简便地运算而已。一般情况下能运用前两种方法就已经够用了。